Finally, the 3rd installment of notes for the Cryptopals crypto challenges. It’s still incomplete but it’s been lying around for ages and I guess I can always come back and edit it.
from binascii import unhexlify, b2a_base64, a2b_base64, hexlify
from base64 import b64decode
from Crypto.Cipher import AES
import random
import string
from collections import defaultdict
import numpy as np
import time
Challenge 17: The CBC Padding Oracle¶
The challenge is to decrypt CBC-encoded text by utilizing information leaked by a padding checker. First we’ll need some of the functions from Set 2.
def generate_random_bytes(num_bytes: int) -> bytes:
return bytes([random.randint(0, 255) for _ in range(num_bytes)])
def fixed_xor(buffer1: bytes, buffer2: bytes) -> bytes:
return bytes([(b1 ^ b2) for b1, b2 in zip(buffer1, buffer2)])
def bytes_to_str(byte_list: bytes) -> str:
return "".join(filter(lambda x: x in string.printable, "".join(map(chr, byte_list))))
def aes_in_ecb_mode(byte_string: bytes, key: bytes, encrypt: bool = False) -> bytes:
cipher = AES.new(key, AES.MODE_ECB)
if encrypt:
return cipher.encrypt(byte_string)
else:
return cipher.decrypt(byte_string)
def pkcs7_padding(byte_string: bytes, block_length: int) -> bytes:
num_to_pad = block_length - (len(byte_string) % block_length)
return byte_string + bytes([num_to_pad]) * num_to_pad
def pkcs7_padding_validation(byte_string: bytes)->bytes:
last_byte = byte_string[-1]
if last_byte > len(byte_string):
raise ValueError("bad padding")
for i in range(last_byte, 0, -1):
if byte_string[-i] != last_byte:
raise ValueError("bad padding")
return byte_string[:-last_byte]
def cbc_mode(byte_string: bytes,
key: bytes,
initialization_vector: bytes,
encrypt: bool = True) -> bytes:
if encrypt:
previous_block = initialization_vector
cipher_text = b''
for i in range(0, len(byte_string), len(key)):
plain_text = fixed_xor(pkcs7_padding(byte_string[i: i + len(key)], len(key)),
previous_block)
previous_block = aes_in_ecb_mode(plain_text, key, encrypt=True)
cipher_text += previous_block
return cipher_text
else:
previous_block = initialization_vector
plain_text = b''
for i in range(0, len(byte_string), len(key)):
cipher_text = byte_string[i: i + len(key)]
plain_text += fixed_xor(aes_in_ecb_mode(cipher_text, key, encrypt=False), previous_block)
previous_block = cipher_text
return plain_text
The encryptor selects a random string from a list of 10 strings, pads it to 16 bytes, and encrypts it in CBC-mode with a random initialization vector. It then returns the encrypted string along with the initialization vector (IV) used.
BLOCK_SIZE = 16
RANDOM_STRINGS = [
b'MDAwMDAwTm93IHRoYXQgdGhlIHBhcnR5IGlzIGp1bXBpbmc=',
b'MDAwMDAxV2l0aCB0aGUgYmFzcyBraWNrZWQgaW4gYW5kIHRoZSBWZWdhJ3MgYXJlIHB1bXBpbic=',
b'MDAwMDAyUXVpY2sgdG8gdGhlIHBvaW50LCB0byB0aGUgcG9pbnQsIG5vIGZha2luZw==',
b'MDAwMDAzQ29va2luZyBNQydzIGxpa2UgYSBwb3VuZCBvZiBiYWNvbg==',
b'MDAwMDA0QnVybmluZyAnZW0sIGlmIHlvdSBhaW4ndCBxdWljayBhbmQgbmltYmxl',
b'MDAwMDA1SSBnbyBjcmF6eSB3aGVuIEkgaGVhciBhIGN5bWJhbA==',
b'MDAwMDA2QW5kIGEgaGlnaCBoYXQgd2l0aCBhIHNvdXBlZCB1cCB0ZW1wbw==',
b'MDAwMDA3SSdtIG9uIGEgcm9sbCwgaXQncyB0aW1lIHRvIGdvIHNvbG8=',
b'MDAwMDA4b2xsaW4nIGluIG15IGZpdmUgcG9pbnQgb2g=',
b'MDAwMDA5aXRoIG15IHJhZy10b3AgZG93biBzbyBteSBoYWlyIGNhbiBibG93']
GLOBAL_KEY = generate_random_bytes(BLOCK_SIZE)
def choose_string():
return pkcs7_padding(RANDOM_STRINGS[random.randint(0, len(RANDOM_STRINGS)-1)],
BLOCK_SIZE)
def cbc_padding_oracle_encrypt(chosen_string=None, print_string=False) -> tuple:
if chosen_string is None:
chosen_string = choose_string()
if print_string:
print(f"Chosen String: {chosen_string}")
initialization_vector = generate_random_bytes(BLOCK_SIZE)
return cbc_mode(chosen_string, GLOBAL_KEY, initialization_vector, encrypt=True), initialization_vector
Then we build our padding oracle which takes this ciphertext as input. It returns True if the ciphertext’s padding is correct and False otherwise.
def cbc_padding_oracle_check(byte_string: bytes, initialization_vector: bytes) -> bool:
decrypted_string = cbc_mode(byte_string, GLOBAL_KEY, initialization_vector, encrypt=False)
try:
pkcs7_padding_validation(decrypted_string)
except ValueError:
return False
else:
return True
encrypted_string, iv = cbc_padding_oracle_encrypt()
print(cbc_padding_oracle_check(encrypted_string, iv))
True
Okay, on to the decryption. First, a refresher of CBC-mode decryption:
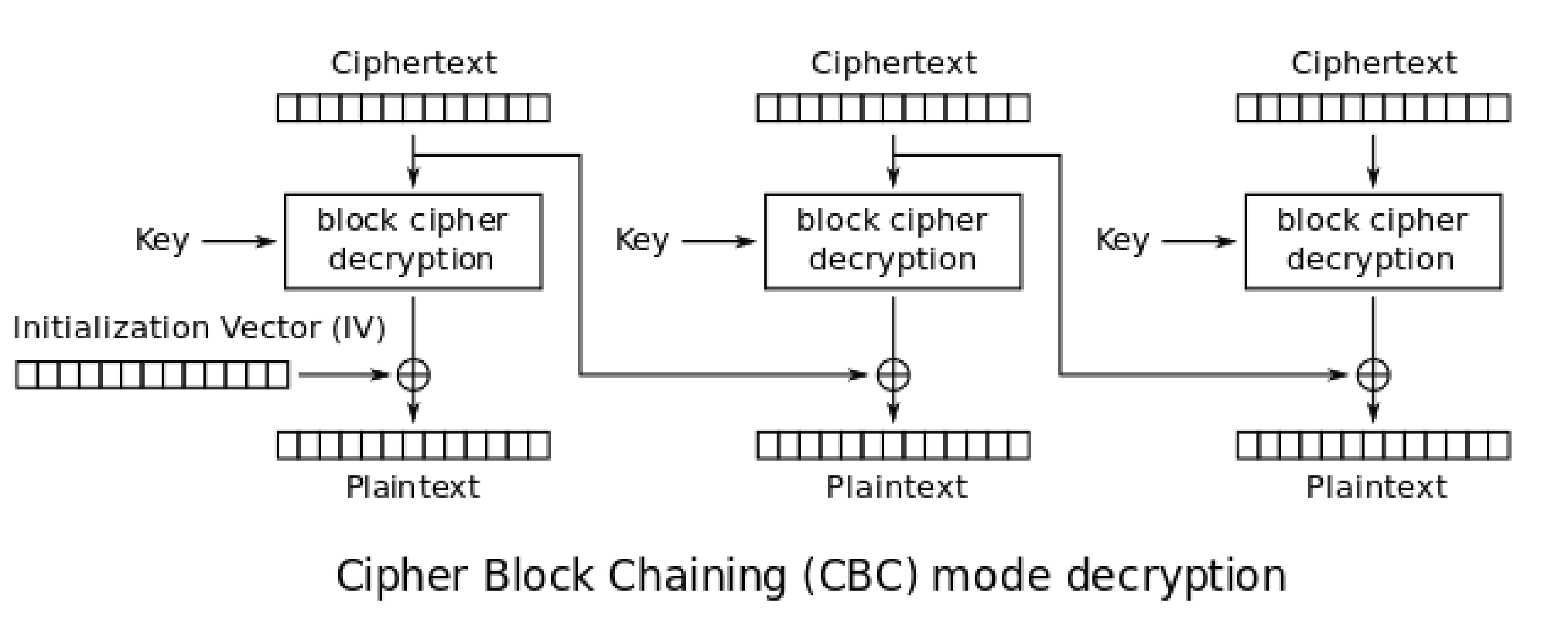
So, the first plaintext block is created by XORing the IV with the decrypted first ciphertext block. Then, the second plaintext block is the XOR of the first ciphertext block with the decrypted second ciphertext block, and so on. Suppose we call our ciphertext blocks $ C_i $ (with $ C_0 $ being the IV, $ C_1$ being the first ciphertext block etc.), and our plaintext blocks $ P_i $ (starting from i=1 as the first plaintext block). Then,
$$ P_1 = decrypt(C_1) \oplus C_0 $$$$ P_2 = decrypt(C_2) \oplus C_1 $$$$ P_i = decrypt(C_i) \oplus C_{i-1} $$The only thing we can modify in this equation are the ciphertext blocks, $ C_i $. But since they’re used to make the plaintext, a single byte change in $ C_0 $ causes a single byte change in $ P_1 $. Sending the byte string of $ C_0 $ concatenated with $ C_1 $ to the padding oracle tells us whether the padding of the decrypted $ P_1 $ is correct.
Let’s say we modify the very last, 16th byte of $ C_0 $ to 0x00 and send the modified $ C_0^*$ concatenated with $ C_1 $ to the padding oracle.
- If the padding oracle returns True, then we know that the last byte of $ decrypt(C_1) \oplus C_0^* $ is
0x01, since that’s the most likely way to get valid padding from a last-byte-messed up plaintext. The second way would be if the last byte of the plaintext becomes0x02and the second last byte just happened to also be0x02which is much less likely (solved by taking both bytes for which the oracle returns True and trying out the next byte for both), and the probability of the case with0x03and higher is negligible. - If the padding oracle returns False, then we change the last byte to
0x01then0x02and so on till it returns True - after all there are only 256 possibilities and we have all the time in the world.
So at some byte value, say 60, as the 16th byte of $ C_0^* $, we have a valid padding of 0x01 for $ P_1^* $. But this means:
$$ decrypt(C_1)[16] = C_0^*[16] \oplus P_1^*[16] = 60 \oplus 01 = 61 \text{ (since $\oplus$s are invertible)}$$
So we have the 16th byte of $ decrypt(C_1) $, which we can plug back in to our original formula to get the 16th byte of plaintext $ P_1 $! $$ P_1[16] = decrypt(C_1[16]) \oplus C_0[16] = 61 \oplus C_0[16] $$
Here’s that in code:
Let’s pick a string first to demonstrate
CHOSEN_STRING = choose_string()
encrypted_string, iv = cbc_padding_oracle_encrypt(chosen_string=CHOSEN_STRING)
C_0 = iv
C_1 = encrypted_string[:BLOCK_SIZE]
d_C_1_16s = []
P_1_16s = []
for b in range(256):
C_0_modified = bytearray(C_0)
C_0_modified[15] = b
if cbc_padding_oracle_check(bytes(C_0_modified) + C_1, iv):
d_C_1_16 = b ^ 1
d_C_1_16s.append(d_C_1_16)
P_1_16 = d_C_1_16 ^ C_0[15]
P_1_16s.append(P_1_16)
print(P_1_16s)
[110, 111]
So, there’s two options for the last byte and both give correct padding. We have to remember this in the next round to check which one is real and which one is an accident.
Repeating this for the next byte wasn’t completely obvious to me but I worked it out eventually. Since we know the value of $ decrypt(C_1)[16] $ we can change the last byte of a new $ P_1^* $ to 0x02 by changing the value of $ C_0^*[16] $:
$$ C_0^*[16] = P_1^*[16] \oplus decrypt(C_1)[16] = 02 \oplus 61 = 63 $$
Now let’s set $ C_0^*[15] $ to 0x00.
- If the padding oracle, again given $ C_0^* $ concatenated with $ C_1 $ returns True, this means $ P_1^*[15] $ is also
0x02since the only way to have a correct padding is if it ends in (0x020x02). - If it returns False we try and try again with all 256 possible byte values.
Then, we do what we did before, this time to find $ decrypt(C_1)[15] $, and then use this value with the original $ C_0[15] $ to get $ P_1[15] $.
for P_1_16, d_C_1_16 in zip(P_1_16s, d_C_1_16s): # this checks both options
C_0_modified_16 = 2 ^ d_C_1_16
for b in range(256):
C_0_modified = bytearray(C_0)
C_0_modified[15] = C_0_modified_16
C_0_modified[14] = b
if cbc_padding_oracle_check(bytes(C_0_modified) + C_1, iv):
d_C_1_15 = b ^ 2
P_1_15 = d_C_1_15 ^ C_0[14]
print(P_1_16, P_1_15)
110 52
Did we get it right?
CHOSEN_STRING[15], CHOSEN_STRING[14]
(110, 52)
Keep going, setting $C_0^*$ such that the last two bytes of $P_1^*$ become 0x03 then finding the byte value that makes the 14th byte also 0x03…
d_C_currents = [d_C_1_15, d_C_1_16]
plaintext_block = [P_1_15, P_1_16]
C_previous = iv
C_current = encrypted_string[:BLOCK_SIZE]
for i in range(BLOCK_SIZE-3, -1, -1):
for b in range(256):
C_previous_modified = bytearray(C_previous)
if len(d_C_currents):
C_previous_modified[-len(d_C_currents):] = [(BLOCK_SIZE - i) ^ d_C_current_i for d_C_current_i in d_C_currents]
C_previous_modified[i] = b
if cbc_padding_oracle_check(bytes(C_previous_modified) + C_current, iv):
d_C_current_i = b ^ (BLOCK_SIZE - i)
P_current_i = d_C_current_i ^ C_previous[i]
plaintext_block = [P_current_i] + plaintext_block
d_C_currents = [d_C_current_i] + d_C_currents
break
print(plaintext_block)
[52, 111]
[b for b in CHOSEN_STRING[:16]]
[77, 68, 65, 119, 77, 68, 65, 52, 98, 50, 120, 115, 97, 87, 52, 110]
Putting all this together into functions:
def cbc_one_byte(C_previous, C_current, i, IV, d_C_currents, break_after_first=True):
P_current_i_possibilities = []
d_C_current_i_possibilities = []
for b in range(256):
C_previous_modified = bytearray(C_previous)
if len(d_C_currents):
C_previous_modified[-len(d_C_currents):] = [(BLOCK_SIZE - i) ^ d_C_current_i for d_C_current_i in d_C_currents]
C_previous_modified[i] = b
if cbc_padding_oracle_check(bytes(C_previous_modified) + C_current, IV):
d_C_current_i = b ^ (BLOCK_SIZE - i)
P_current_i = d_C_current_i ^ C_previous[i]
P_current_i_possibilities.append(P_current_i)
d_C_current_i_possibilities.append(d_C_current_i)
if break_after_first:
break
return P_current_i_possibilities, d_C_current_i_possibilities
def cbc_one_block(C_previous, C_current, IV):
plaintext_block = []
d_C_currents = []
P_current_16s, d_C_current_16s = cbc_one_byte(C_previous, C_current, 15, IV, [], break_after_first=False)
for P_current_16, d_C_current_16 in zip(P_current_16s, d_C_current_16s):
P_current_15s, d_C_current_15s = cbc_one_byte(C_previous, C_current, 14, IV, [d_C_current_16], break_after_first=True)
if len(P_current_15s):
plaintext_block = [P_current_15s[0], P_current_16]
d_C_currents = [d_C_current_15s[0], d_C_current_16]
break
for i in range(BLOCK_SIZE-3, -1, -1):
P_current_is, d_C_current_is = cbc_one_byte(C_previous, C_current, i, IV, d_C_currents, break_after_first=True)
plaintext_block = [P_current_is[0]] + plaintext_block
d_C_currents = [d_C_current_is[0]] + d_C_currents
return plaintext_block
Repeat for the other blocks and we’re done!
def cbc_padding_oracle_attack(encrypted_string, IV, padding_oracle) -> bytes:
num_blocks = len(encrypted_string) // BLOCK_SIZE
plaintext_blocks = []
C_previous = IV
for n in range(num_blocks):
C_current = encrypted_string[n*BLOCK_SIZE: (n+1)*BLOCK_SIZE]
plaintext_block = cbc_one_block(C_previous, C_current, IV)
plaintext_blocks.append(bytes(plaintext_block))
C_previous = C_current
return b''.join(plaintext_blocks)
decrypted_string = cbc_padding_oracle_attack(encrypted_string, iv, cbc_padding_oracle_check)
CHOSEN_STRING == decrypted_string
True
Challenge 18: Implement CTR, the stream cipher mode¶
Another AES block cipher mode! It’s pretty well explained on the problem page so I won’t go into much detail. This one is a bit smarter though - it encrypts an incrementing counter to make a streaming key which is then XORed against the plaintext. Decryption is exactly the same, you don’t even need an extra function or flag. “Nonce” here is similar to the initialization vectors from before - it’s concatenated with the current count to randomize things a bit more.
def ctr_keystream(key: bytes, nonce: int):
counter = 0
nonce_bytes = nonce.to_bytes(BLOCK_SIZE // 2, byteorder='little')
while True:
counter_bytes = counter.to_bytes(BLOCK_SIZE // 2, byteorder='little')
yield from aes_in_ecb_mode(nonce_bytes + counter_bytes,
key, encrypt=True)
counter += 1
def ctr_mode(byte_string: bytes, key: bytes, nonce: int) -> bytes:
if len(byte_string) == 0:
return b''
return fixed_xor(byte_string, ctr_keystream(key, nonce))
ctr_mode(b64decode('L77na/nrFsKvynd6HzOoG7GHTLXsTVu9qvY/2syLXzhPweyyMTJULu/6/kXX0KSvoOLSFQ=='),
b'YELLOW SUBMARINE',
nonce=0)
b"Yo, VIP Let's kick it Ice, Ice, baby Ice, Ice, baby "
Heheh “something approximating English”.
Challenge 19: Break fixed-nonce CTR mode using substitutions¶
So this one is to show us how using the same nonce to encrypt different sets of data is baaaad. It’s not really an algorithm, more like try stuff out till stuff makes sense. Here’s a small snapshot of how I worked:
random_key = generate_random_bytes(16)
with open("data/crypto/19.txt") as f:
ciphertexts = [ctr_mode(a2b_base64(line.strip()), key=random_key, nonce=0) for line in f]
min_length = min(len(c) for c in ciphertexts)
max_length = max(len(c) for c in ciphertexts)
real_keystream = [x for _, x in zip(range(max_length),
ctr_keystream(key=random_key, nonce=0))]
predicted_keystream = [0]*len(real_keystream)
First, we make a function that prints ranges of letters that are shared across ciphertexts.
def count_kgrams(k, greater_than=2):
print("\t\t".join(("pos", "count", "ciphertext")))
for m in range(min_length - k):
column = defaultdict(list)
for i, c in enumerate(ciphertexts):
column[c[m: m+k]].append(i)
keys = list(column.keys())
counts = np.argsort([len(column[k]) for k in keys])[::-1]
for index in counts[:3]:
count = len(column[keys[index]])
if count > greater_than:
print('\t\t'.join(str(x) for x in [list(range(m, m+k)), count, column[keys[index]]]))
# Count monograms
count_kgrams(1, greater_than=9)
pos count ciphertext [2] 11 [5, 6, 9, 10, 17, 27, 28, 29, 32, 33, 36] [3] 10 [8, 13, 14, 18, 22, 24, 26, 34, 35, 37] [6] 10 [2, 8, 9, 16, 17, 20, 21, 35, 37, 38] [10] 11 [0, 11, 15, 18, 20, 21, 25, 26, 30, 31, 39] [12] 10 [2, 9, 14, 16, 23, 24, 28, 34, 35, 37]
The most common monogram is ‘e’, followed by ‘t’, ‘a’, and ‘o’. First let’s put in ‘e’ for all these most common monograms using one of the ciphertexts that they appear in
def print_solved_ciphertexts(solved_columns):
print(' ' + '|'.join(str(i) for i in range(min_length)))
for i, ciphertext in enumerate(ciphertexts):
print(f'{i:02} ' + '|'.join(chr(x) if j in solved_columns else '_' for j, x in enumerate(fixed_xor(ciphertext, predicted_keystream))))
predicted_keystream[2] = ciphertexts[5][2] ^ ord('e')
predicted_keystream[3] = ciphertexts[8][3] ^ ord('e')
predicted_keystream[6] = ciphertexts[2][6] ^ ord('e')
predicted_keystream[10] = ciphertexts[0][10] ^ ord('e')
predicted_keystream[12] = ciphertexts[2][12] ^ ord('e')
solved_columns = {2,3,6,10,12}
print_solved_ciphertexts(solved_columns)
0|1|2|3|4|5|6|7|8|9|10|11|12|13|14|15|16|17|18|19 00 _|_|-|$|_|_|*|_|_|_|e|_|-|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 01 _|_|(|,|_|_|*|_|_|_|-|_|3|_|_|_|_|_|_|_|_|_|_ 02 _|_|*|(|_|_|e|_|_|_| |_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 03 _|_|"|-|_|_|o|_|_|_|h|_| |_|_|_|_|_|_|_|_|_|_|_|_|_ 04 _|_|-|$|_|_|*|_|_|_|6|_|!|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 05 _|_|e|5|_|_|c|_|_|_|(|_|$|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 06 _|_|e|-|_|_|o|_|_|_|+|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 07 _|_|)|,|_|_|*|_|_|_|+|_|+|_|_|_|_|_|_|_|_|_|_|_|_ 08 _|_|!|e|_|_|e|_|_|_|1|_|'|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 09 _|_|e|$|_|_|e|_|_|_|+|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 10 _|_|e|5|_|_|k|_|_|_|$|_|&|_|_|_|_|_|_|_|_ 11 _|_|*|0|_|_|*|_|_|_|e|_|,|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 12 _|_|,|+|_|_|i|_|_|_|$|_|+|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 13 _|_|1|e|_|_|||_|_|_|2|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 14 _|_|)|e|_|_|k|_|_|_|!|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 15 _|_|1| |_|_|c|_|_|_|e|_| |_|_|_|_|_|_|_|_|_|_|_|_|_ 16 _|_|$|1|_|_|e|_|_|_|b|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 17 _|_|e|,|_|_|e|_|_|_|1|_|"|_|_|_|_|_|_|_|_|_ 18 _|_|7|e|_|_|m|_|_|_|e|_|+|_|_|_|_|_|_|_|_|_ 19 _|_|1|,|_|_|b|_|_|_|3|_|,|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 20 _|_|$|1|_|_|e|_|_|_|e|_|*|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 21 _|_| |+|_|_|e|_|_|_|e|_|+|_|_|_|_|_|_|_|_|_|_|_|_ 22 _|_| |e|_|_|n|_|_|_|*|_|-|_|_|_|_|_|_|_|_ 23 _|_|,|6|_|_|k|_|_|_|$|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_ 24 _|_|!|e|_|_|n|_|_|_|0|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_ 25 _|_|,|6|_|_|~|_|_|_|e|_|,|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 26 _|_|6|e|_|_|g|_|_|_|e|_|+|_|_|_|_|_|_|_|_|_|_|_|_|_ 27 _|_|e|(|_|_|b|_|_|_|$|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 28 _|_|e|6|_|_|y|_|_|_|3|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 29 _|_|e|!|_|_|c|_|_|_|$|_|!|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 30 _|_|,|6|_|_|~|_|_|_|e|_|$|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 31 _|_|!|7|_|_|a|_|_|_|e|_|$|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 32 _|_|e|-|_|_|*|_|_|_| |_|(|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 33 _|_|e|6|_|_|o|_|_|_|*|_|$|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 34 _|_|1|e|_|_|d|_|_|_| |_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 35 _|_|i|e|_|_|e|_|_|_|$|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 36 _|_|e|1|_|_|*|_|_|_|0|_|)|_|_|_|_|_|_|_|_ 37 _|_|i|e|_|_|e|_|_|_|$|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 38 _|_|$|+|_|_|e|_|_|_|!|_|0|_|_|_|_|_|_|_ 39 _|_|1| |_|_|c|_|_|_|e|_| |_|_|_|_|_|_|_|_|_|_|_|_|_
Hmm, looks like none of them are ‘e’s since putting in the ‘e’ made the other letters in that column rubbish. Wait, we’ve been bitten by this before! Spaces are way more common than letters!
predicted_keystream[2] = ciphertexts[5][2] ^ ord(' ')
predicted_keystream[3] = ciphertexts[8][3] ^ ord(' ')
predicted_keystream[6] = ciphertexts[8][6] ^ ord(' ')
predicted_keystream[10] = ciphertexts[0][10] ^ ord(' ')
predicted_keystream[12] = ciphertexts[2][12] ^ ord(' ')
print_solved_ciphertexts(solved_columns)
0|1|2|3|4|5|6|7|8|9|10|11|12|13|14|15|16|17|18|19 00 _|_|h|a|_|_|o|_|_|_| |_|h|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 01 _|_|m|i|_|_|o|_|_|_|h|_|v|_|_|_|_|_|_|_|_|_|_ 02 _|_|o|m|_|_| |_|_|_|e|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 03 _|_|g|h|_|_|*|_|_|_|-|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_ 04 _|_|h|a|_|_|o|_|_|_|s|_|d|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 05 _|_| |p|_|_|&|_|_|_|m|_|a|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 06 _|_| |h|_|_|*|_|_|_|n|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 07 _|_|l|i|_|_|o|_|_|_|n|_|n|_|_|_|_|_|_|_|_|_|_|_|_ 08 _|_|d| |_|_| |_|_|_|t|_|b|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 09 _|_| |a|_|_| |_|_|_|n|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_ 10 _|_| |p|_|_|.|_|_|_|a|_|c|_|_|_|_|_|_|_|_ 11 _|_|o|u|_|_|o|_|_|_| |_|i|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 12 _|_|i|n|_|_|,|_|_|_|a|_|n|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 13 _|_|t| |_|_|9|_|_|_|w|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 14 _|_|l| |_|_|.|_|_|_|d|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 15 _|_|t|e|_|_|&|_|_|_| |_|e|_|_|_|_|_|_|_|_|_|_|_|_|_ 16 _|_|a|t|_|_| |_|_|_|'|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 17 _|_| |i|_|_| |_|_|_|t|_|g|_|_|_|_|_|_|_|_|_ 18 _|_|r| |_|_|(|_|_|_| |_|n|_|_|_|_|_|_|_|_|_ 19 _|_|t|i|_|_|'|_|_|_|v|_|i|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 20 _|_|a|t|_|_| |_|_|_| |_|o|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 21 _|_|e|n|_|_| |_|_|_| |_|n|_|_|_|_|_|_|_|_|_|_|_|_ 22 _|_|e| |_|_|+|_|_|_|o|_|h|_|_|_|_|_|_|_|_ 23 _|_|i|s|_|_|.|_|_|_|a|_| |_|_|_|_|_|_|_|_|_|_|_|_|_ 24 _|_|d| |_|_|+|_|_|_|u|_| |_|_|_|_|_|_|_|_|_|_|_|_|_ 25 _|_|i|s|_|_|;|_|_|_| |_|i|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 26 _|_|s| |_|_|"|_|_|_| |_|n|_|_|_|_|_|_|_|_|_|_|_|_|_ 27 _|_| |m|_|_|'|_|_|_|a|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 28 _|_| |s|_|_|<|_|_|_|v|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 29 _|_| |d|_|_|&|_|_|_|a|_|d|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 30 _|_|i|s|_|_|;|_|_|_| |_|a|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 31 _|_|d|r|_|_|$|_|_|_| |_|a|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 32 _|_| |h|_|_|o|_|_|_|e|_|m|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 33 _|_| |s|_|_|*|_|_|_|o|_|a|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 34 _|_|t| |_|_|!|_|_|_|e|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 35 _|_|,| |_|_| |_|_|_|a|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 36 _|_| |t|_|_|o|_|_|_|u|_|l|_|_|_|_|_|_|_|_ 37 _|_|,| |_|_| |_|_|_|a|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 38 _|_|a|n|_|_| |_|_|_|d|_|u|_|_|_|_|_|_|_ 39 _|_|t|e|_|_|&|_|_|_| |_|e|_|_|_|_|_|_|_|_|_|_|_|_|_
That’s more like it. Columns 2, 3, 10 and 12 make sense. 6 doesn’t though. Maybe 6 is ‘t’ or ‘a’ or ‘o’?
predicted_keystream[6] = ciphertexts[8][6] ^ ord('o')
print_solved_ciphertexts(solved_columns)
0|1|2|3|4|5|6|7|8|9|10|11|12|13|14|15|16|17|18|19 00 _|_|h|a|_|_| |_|_|_| |_|h|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 01 _|_|m|i|_|_| |_|_|_|h|_|v|_|_|_|_|_|_|_|_|_|_ 02 _|_|o|m|_|_|o|_|_|_|e|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 03 _|_|g|h|_|_|e|_|_|_|-|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_ 04 _|_|h|a|_|_| |_|_|_|s|_|d|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 05 _|_| |p|_|_|i|_|_|_|m|_|a|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 06 _|_| |h|_|_|e|_|_|_|n|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 07 _|_|l|i|_|_| |_|_|_|n|_|n|_|_|_|_|_|_|_|_|_|_|_|_ 08 _|_|d| |_|_|o|_|_|_|t|_|b|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 09 _|_| |a|_|_|o|_|_|_|n|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_ 10 _|_| |p|_|_|a|_|_|_|a|_|c|_|_|_|_|_|_|_|_ 11 _|_|o|u|_|_| |_|_|_| |_|i|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 12 _|_|i|n|_|_|c|_|_|_|a|_|n|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 13 _|_|t| |_|_|v|_|_|_|w|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 14 _|_|l| |_|_|a|_|_|_|d|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 15 _|_|t|e|_|_|i|_|_|_| |_|e|_|_|_|_|_|_|_|_|_|_|_|_|_ 16 _|_|a|t|_|_|o|_|_|_|'|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 17 _|_| |i|_|_|o|_|_|_|t|_|g|_|_|_|_|_|_|_|_|_ 18 _|_|r| |_|_|g|_|_|_| |_|n|_|_|_|_|_|_|_|_|_ 19 _|_|t|i|_|_|h|_|_|_|v|_|i|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 20 _|_|a|t|_|_|o|_|_|_| |_|o|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 21 _|_|e|n|_|_|o|_|_|_| |_|n|_|_|_|_|_|_|_|_|_|_|_|_ 22 _|_|e| |_|_|d|_|_|_|o|_|h|_|_|_|_|_|_|_|_ 23 _|_|i|s|_|_|a|_|_|_|a|_| |_|_|_|_|_|_|_|_|_|_|_|_|_ 24 _|_|d| |_|_|d|_|_|_|u|_| |_|_|_|_|_|_|_|_|_|_|_|_|_ 25 _|_|i|s|_|_|t|_|_|_| |_|i|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 26 _|_|s| |_|_|m|_|_|_| |_|n|_|_|_|_|_|_|_|_|_|_|_|_|_ 27 _|_| |m|_|_|h|_|_|_|a|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 28 _|_| |s|_|_|s|_|_|_|v|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 29 _|_| |d|_|_|i|_|_|_|a|_|d|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 30 _|_|i|s|_|_|t|_|_|_| |_|a|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 31 _|_|d|r|_|_|k|_|_|_| |_|a|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 32 _|_| |h|_|_| |_|_|_|e|_|m|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 33 _|_| |s|_|_|e|_|_|_|o|_|a|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 34 _|_|t| |_|_|n|_|_|_|e|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 35 _|_|,| |_|_|o|_|_|_|a|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 36 _|_| |t|_|_| |_|_|_|u|_|l|_|_|_|_|_|_|_|_ 37 _|_|,| |_|_|o|_|_|_|a|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 38 _|_|a|n|_|_|o|_|_|_|d|_|u|_|_|_|_|_|_|_ 39 _|_|t|e|_|_|i|_|_|_| |_|e|_|_|_|_|_|_|_|_|_|_|_|_|_
Let’s take a look at higher order k-grams
# Count trigrams
count_kgrams(3, greater_than=2)
pos count ciphertext [0, 1, 2] 3 [23, 25, 30] [1, 2, 3] 3 [23, 25, 30] [2, 3, 4] 3 [23, 25, 30] [8, 9, 10] 4 [23, 27, 35, 37] [13, 14, 15] 4 [11, 13, 20, 33] [16, 17, 18] 3 [0, 11, 12]
Looks like 13-15 is a three letter word.
# Count 5-grams
count_kgrams(5, greater_than=2)
pos count ciphertext [0, 1, 2, 3, 4] 3 [23, 25, 30]
0-4 is a 5-letter word common to ciphertexts 23, 25, and 30 and it also has ‘is’ in the middle (from the previous output). Could it be ‘This ‘?
predicted_keystream[0:5] = fixed_xor(ciphertexts[23][0:5], b'This ')
solved_columns = solved_columns.union((0, 1, 2, 3, 4))
print_solved_ciphertexts(solved_columns)
0|1|2|3|4|5|6|7|8|9|10|11|12|13|14|15|16|17|18|19 00 I| |h|a|v|_| |_|_|_| |_|h|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 01 C|o|m|i|n|_| |_|_|_|h|_|v|_|_|_|_|_|_|_|_|_|_ 02 F|r|o|m| |_|o|_|_|_|e|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 03 E|i|g|h|t|_|e|_|_|_|-|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_ 04 I| |h|a|v|_| |_|_|_|s|_|d|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 05 O|r| |p|o|_|i|_|_|_|m|_|a|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 06 O|r| |h|a|_|e|_|_|_|n|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 07 P|o|l|i|t|_| |_|_|_|n|_|n|_|_|_|_|_|_|_|_|_|_|_|_ 08 A|n|d| |t|_|o|_|_|_|t|_|b|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 09 O|f| |a| |_|o|_|_|_|n|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_ 10 T|o| |p|l|_|a|_|_|_|a|_|c|_|_|_|_|_|_|_|_ 11 A|r|o|u|n|_| |_|_|_| |_|i|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 12 B|e|i|n|g|_|c|_|_|_|a|_|n|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 13 B|u|t| |l|_|v|_|_|_|w|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 14 A|l|l| |c|_|a|_|_|_|d|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 15 A| |t|e|r|_|i|_|_|_| |_|e|_|_|_|_|_|_|_|_|_|_|_|_|_ 16 T|h|a|t| |_|o|_|_|_|'|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 17 I|n| |i|g|_|o|_|_|_|t|_|g|_|_|_|_|_|_|_|_|_ 18 H|e|r| |n|_|g|_|_|_| |_|n|_|_|_|_|_|_|_|_|_ 19 U|n|t|i|l|_|h|_|_|_|v|_|i|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 20 W|h|a|t| |_|o|_|_|_| |_|o|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 21 W|h|e|n| |_|o|_|_|_| |_|n|_|_|_|_|_|_|_|_|_|_|_|_ 22 S|h|e| |r|_|d|_|_|_|o|_|h|_|_|_|_|_|_|_|_ 23 T|h|i|s| |_|a|_|_|_|a|_| |_|_|_|_|_|_|_|_|_|_|_|_|_ 24 A|n|d| |r|_|d|_|_|_|u|_| |_|_|_|_|_|_|_|_|_|_|_|_|_ 25 T|h|i|s| |_|t|_|_|_| |_|i|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 26 W|a|s| |c|_|m|_|_|_| |_|n|_|_|_|_|_|_|_|_|_|_|_|_|_ 27 H|e| |m|i|_|h|_|_|_|a|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 28 S|o| |s|e|_|s|_|_|_|v|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 29 S|o| |d|a|_|i|_|_|_|a|_|d|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 30 T|h|i|s| |_|t|_|_|_| |_|a|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 31 A| |d|r|u|_|k|_|_|_| |_|a|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 32 H|e| |h|a|_| |_|_|_|e|_|m|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 33 T|o| |s|o|_|e|_|_|_|o|_|a|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 34 Y|e|t| |I|_|n|_|_|_|e|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 35 H|e|,| |t|_|o|_|_|_|a|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 36 I|n| |t|h|_| |_|_|_|u|_|l|_|_|_|_|_|_|_|_ 37 H|e|,| |t|_|o|_|_|_|a|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 38 T|r|a|n|s|_|o|_|_|_|d|_|u|_|_|_|_|_|_|_ 39 A| |t|e|r|_|i|_|_|_| |_|e|_|_|_|_|_|_|_|_|_|_|_|_|_
Oh boy, we’re well on our way now.
predicted_keystream[5] = ciphertexts[0][5] ^ ord('e')
predicted_keystream[7] = ciphertexts[39][7] ^ ord('b')
predicted_keystream[8] = ciphertexts[38][8] ^ ord('m')
solved_columns.add(5)
solved_columns.add(7)
solved_columns.add(8)
print_solved_ciphertexts(solved_columns)
0|1|2|3|4|5|6|7|8|9|10|11|12|13|14|15|16|17|18|19 00 I| |h|a|v|e| |m|e|_| |_|h|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 01 C|o|m|i|n|g| |w|i|_|h|_|v|_|_|_|_|_|_|_|_|_|_ 02 F|r|o|m| |c|o|u|n|_|e|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 03 E|i|g|h|t|e|e|n|t|_|-|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_ 04 I| |h|a|v|e| |p|a|_|s|_|d|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 05 O|r| |p|o|l|i|t|e|_|m|_|a|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 06 O|r| |h|a|v|e| |l|_|n|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 07 P|o|l|i|t|e| |m|e|_|n|_|n|_|_|_|_|_|_|_|_|_|_|_|_ 08 A|n|d| |t|h|o|u|g|_|t|_|b|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 09 O|f| |a| |m|o|c|k|_|n|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_ 10 T|o| |p|l|e|a|s|e|_|a|_|c|_|_|_|_|_|_|_|_ 11 A|r|o|u|n|d| |t|h|_| |_|i|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 12 B|e|i|n|g| |c|e|r|_|a|_|n|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 13 B|u|t| |l|i|v|e|d|_|w|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 14 A|l|l| |c|h|a|n|g|_|d|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 15 A| |t|e|r|r|i|b|l|_| |_|e|_|_|_|_|_|_|_|_|_|_|_|_|_ 16 T|h|a|t| |w|o|m|a|_|'|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 17 I|n| |i|g|n|o|r|a|_|t|_|g|_|_|_|_|_|_|_|_|_ 18 H|e|r| |n|i|g|h|t|_| |_|n|_|_|_|_|_|_|_|_|_ 19 U|n|t|i|l| |h|e|r|_|v|_|i|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 20 W|h|a|t| |v|o|i|c|_| |_|o|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 21 W|h|e|n| |y|o|u|n|_| |_|n|_|_|_|_|_|_|_|_|_|_|_|_ 22 S|h|e| |r|o|d|e| |_|o|_|h|_|_|_|_|_|_|_|_ 23 T|h|i|s| |m|a|n| |_|a|_| |_|_|_|_|_|_|_|_|_|_|_|_|_ 24 A|n|d| |r|o|d|e| |_|u|_| |_|_|_|_|_|_|_|_|_|_|_|_|_ 25 T|h|i|s| |o|t|h|e|_| |_|i|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 26 W|a|s| |c|o|m|i|n|_| |_|n|_|_|_|_|_|_|_|_|_|_|_|_|_ 27 H|e| |m|i|g|h|t| |_|a|_|e|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 28 S|o| |s|e|n|s|i|t|_|v|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 29 S|o| |d|a|r|i|n|g|_|a|_|d|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 30 T|h|i|s| |o|t|h|e|_| |_|a|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 31 A| |d|r|u|n|k|e|n|_| |_|a|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 32 H|e| |h|a|d| |d|o|_|e|_|m|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 33 T|o| |s|o|m|e| |w|_|o|_|a|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 34 Y|e|t| |I| |n|u|m|_|e|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 35 H|e|,| |t|o|o|,| |_|a|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 36 I|n| |t|h|e| |c|a|_|u|_|l|_|_|_|_|_|_|_|_ 37 H|e|,| |t|o|o|,| |_|a|_| |_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 38 T|r|a|n|s|f|o|r|m|_|d|_|u|_|_|_|_|_|_|_ 39 A| |t|e|r|r|i|b|l|_| |_|e|_|_|_|_|_|_|_|_|_|_|_|_|_
Extremely messy and probabilistic, but hey I had most of the songsheet decoded in ~10 minutes. So yeah, point made - randomize your nonces.
Challenge 20: Break fixed-nonce CTR mode using substitutions¶
Ahah! So you can automate the mess from the last problem - using the same techniques we used to break repeating-key XOR (in Set 1) because when your nonce is fixed, CTR is effectively repeating-key XOR with the key being the whole keystream - which is fixed for all the strings (upto the length of the smallest string).
ENGLISH_CHARACTER_FREQUENCY = {'E': 12.70, 'T': 9.06, 'A': 8.17, 'O': 7.51, 'I': 6.97, 'N': 6.75, 'S': 6.33,
'H': 6.09,
'R': 5.99, 'D': 4.25, 'L': 4.03, 'C': 2.78, 'U': 2.76, 'M': 2.41, 'W': 2.36,
'F': 2.23,
'G': 2.02, 'Y': 1.97, 'P': 1.93, 'B': 1.29, 'V': 0.98, 'K': 0.77, 'J': 0.15,
'X': 0.15,
'Q': 0.10, 'Z': 0.07, ' ': 35}
def single_byte_xor_cipher(byte_string: bytes) -> tuple:
strings = [fixed_xor(byte_string, bytearray(bytes([num]) * len(byte_string))) for num in range(256)]
scores = [
sum([bytes_to_str(s).upper().count(c) * ENGLISH_CHARACTER_FREQUENCY[c] for c in ENGLISH_CHARACTER_FREQUENCY])
for s in strings]
index = max(range(len(scores)), key=scores.__getitem__)
return strings[index], max(scores), index
def break_repeating_key_xor(byte_string, keysize):
byte_blocks = [byte_string[i * keysize: (i + 1) * keysize] for i in range(len(byte_string) // keysize)]
transposed_blocks = [bytearray([b[i] for b in byte_blocks]) for i in range(keysize)]
keys = []
for block in transposed_blocks:
_, _, index = single_byte_xor_cipher(block)
keys.append(index)
key = bytearray(keys)
return [x for x in key]
predicted_keystream_min = break_repeating_key_xor(b''.join(c[:min_length] for c in ciphertexts),
keysize=min_length)
predicted_keystream[:min_length] = predicted_keystream_min
solved_columns = set(range(min_length))
print_solved_ciphertexts(solved_columns)
0|1|2|3|4|5|6|7|8|9|10|11|12|13|14|15|16|17|18|19 00 I| |h|a|v|e| |m|e|t| |t|h|e|m| |a|t| |c|_|_|_|_|_|_|_|_|_|_|_ 01 C|o|m|i|n|g| |w|i|t|h| |v|i|v|i|d| |f|a|_|_|_ 02 F|r|o|m| |c|o|u|n|t|e|r| |o|r| |d|e|s|k|_|_|_|_|_|_|_|_|_|_|_ 03 E|i|g|h|t|e|e|n|t|h|-|c|e|n|t|u|r|y| |h|_|_|_|_|_|_ 04 I| |h|a|v|e| |p|a|s|s|e|d| |w|i|t|h| |a|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 05 O|r| |p|o|l|i|t|e| |m|e|a|n|i|n|g|l|e|s|_|_|_|_|_|_|_|_ 06 O|r| |h|a|v|e| |l|i|n|g|e|r|e|d| |a|w|h|_|_|_|_|_|_|_|_|_|_|_|_ 07 P|o|l|i|t|e| |m|e|a|n|i|n|g|l|e|s|s| |w|_|_|_|_|_ 08 A|n|d| |t|h|o|u|g|h|t| |b|e|f|o|r|e| |I|_|_|_|_|_|_|_|_|_ 09 O|f| |a| |m|o|c|k|i|n|g| |t|a|l|e| |o|r|_|_|_|_|_|_|_ 10 T|o| |p|l|e|a|s|e| |a| |c|o|m|p|a|n|i|o|_ 11 A|r|o|u|n|d| |t|h|e| |f|i|r|e| |a|t| |t|_|_|_|_|_|_|_|_ 12 B|e|i|n|g| |c|e|r|t|a|i|n| |t|h|a|t| |t|_|_|_|_|_|_|_|_|_ 13 B|u|t| |l|i|v|e|d| |w|h|e|r|e| |m|o|t|l|_|_|_|_|_|_|_|_|_|_|_ 14 A|l|l| |c|h|a|n|g|e|d|,| |c|h|a|n|g|e|d|_|_|_|_|_|_|_|_|_ 15 A| |t|e|r|r|i|b|l|e| |b|e|a|u|t|y| |i|s|_|_|_|_|_|_ 16 T|h|a|t| |w|o|m|a|n|'|s| |d|a|y|s| |w|e|_|_|_|_|_|_|_|_ 17 I|n| |i|g|n|o|r|a|n|t| |g|o|o|d| |w|i|l|_|_ 18 H|e|r| |n|i|g|h|t|s| |i|n| |a|r|g|u|m|e|_|_ 19 U|n|t|i|l| |h|e|r| |v|o|i|c|e| |g|r|e|w|_|_|_|_|_|_|_|_ 20 W|h|a|t| |v|o|i|c|e| |m|o|r|e| |s|w|e|e|_|_|_|_|_|_|_|_|_|_|_ 21 W|h|e|n| |y|o|u|n|g| |a|n|d| |b|e|a|u|t|_|_|_|_|_ 22 S|h|e| |r|o|d|e| |t|o| |h|a|r|r|i|e|r|s|_ 23 T|h|i|s| |m|a|n| |h|a|d| |k|e|p|t| |a| |_|_|_|_|_|_ 24 A|n|d| |r|o|d|e| |o|u|r| |w|i|n|g|e|d| |_|_|_|_|_|_ 25 T|h|i|s| |o|t|h|e|r| |h|i|s| |h|e|l|p|e|_|_|_|_|_|_|_|_|_|_|_|_ 26 W|a|s| |c|o|m|i|n|g| |i|n|t|o| |h|i|s| |_|_|_|_|_|_ 27 H|e| |m|i|g|h|t| |h|a|v|e| |w|o|n| |f|a|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 28 S|o| |s|e|n|s|i|t|i|v|e| |h|i|s| |n|a|t|_|_|_|_|_|_|_|_|_|_|_ 29 S|o| |d|a|r|i|n|g| |a|n|d| |s|w|e|e|t| |_|_|_|_|_|_|_|_|_|_|_|_ 30 T|h|i|s| |o|t|h|e|r| |m|a|n| |I| |h|a|d|_|_|_|_|_|_|_|_ 31 A| |d|r|u|n|k|e|n|,| |v|a|i|n|-|g|l|o|r|_|_|_|_|_|_|_|_|_|_ 32 H|e| |h|a|d| |d|o|n|e| |m|o|s|t| |b|i|t|_|_|_|_|_|_|_|_|_ 33 T|o| |s|o|m|e| |w|h|o| |a|r|e| |n|e|a|r|_|_|_|_|_|_|_|_|_|_ 34 Y|e|t| |I| |n|u|m|b|e|r| |h|i|m| |i|n| |_|_|_|_|_|_|_|_|_ 35 H|e|,| |t|o|o|,| |h|a|s| |r|e|s|i|g|n|e|_|_|_|_|_|_|_|_|_|_ 36 I|n| |t|h|e| |c|a|s|u|a|l| |c|o|m|e|d|y|_ 37 H|e|,| |t|o|o|,| |h|a|s| |b|e|e|n| |c|h|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_|_ 38 T|r|a|n|s|f|o|r|m|e|d| |u|t|t|e|r|l|y|: 39 A| |t|e|r|r|i|b|l|e| |b|e|a|u|t|y| |i|s|_|_|_|_|_|_
def _int32(x):
return int(0xFFFFFFFF & x)
class MT19937MersenneTwisterRNG:
def __init__(self, seed: int = None):
self.w = 32
self.n = 624
self.m = 397
self.r = 31
self.a = 0x9908B0DF
self.u = 11
self.d = 0xFFFFFFFF
self.s = 7
self.b = 0x9D2C5680
self.t = 15
self.c = 0xEFC60000
self.l = 18
self.f = 1812433253
self.mt = [0]*self.n
self.lower_mask = (1 << self.r) - 1
self.upper_mask = _int32(~self.lower_mask)
if seed is None:
self.seed = 5489
else:
self.seed = seed
self.index = self.n
self.initialize_with_seed()
def initialize_with_seed(self):
self.mt[0] = self.seed
for i in range(1, self.n):
self.mt[i] = _int32(self.f * (self.mt[i-1] ^ (self.mt[i-1] >> (self.w - 2))) + i)
def extract_number(self):
if self.index >= self.n:
self.twist()
y = self.mt[self.index]
y = y ^ ((y >> self.u) & self.d)
y = y ^ ((y << self.s) & self.b)
y = y ^ ((y << self.t) & self.c)
y = y ^ (y >> self.l)
self.index += 1
return _int32(y)
def twist(self):
for i in range(self.n):
x = _int32((self.mt[i] & self.upper_mask) + (self.mt[(i+1) % self.n] & self.lower_mask))
xa = x >> 1
if x % 2 != 0:
xa = xa ^ self.a
self.mt[i] = self.mt[(i + self.m) % self.n] ^ xa
self.index = 0
Challenge 22: Crack an MT19937 seed¶
Now we’re back to the usual flow of things - make a function that does some things and spits out a value, then make another function to figure out what was used to make that value.
First off, we write a function that sleeps for a bit, seeds our previously coded Mersenne Twister RNG with the current time, sleeps again, and finally spits out a random number using the RNG (and also the seed, for validation).
def mt19937_timestamp_seed():
time.sleep(random.randint(4, 100))
seed = int(time.time())
rng = MT19937MersenneTwisterRNG(seed)
time.sleep(random.randint(4, 100))
return rng.extract_number(), seed
Now it’s time to break it. Since it’s time based, we just have to try out previous seconds as seeds! It’s simple because there’s no twisting going on, it’s literally the first number that the RNG spits out after being initialized. If we’d made it output some nth number discarding the ones before then you’d have to iterate over some arbitrary n as well which would be annoying. I think another factor at play here is that no one would be willing to wait more than 2000 or so seconds to get a random number so there’s not an arbitrarily large number of seconds to sift through.
def break_mt19937_seed(rng_function):
random_number, real_seed = rng_function()
now = int(time.time())
before = now - 220
for seed in range(before, now):
rng = MT19937MersenneTwisterRNG(seed)
number = rng.extract_number()
if number == random_number:
print(seed == real_seed)
return seed
break_mt19937_seed(mt19937_timestamp_seed)
True
1577214974
Here’s Set 4