SPOILER WARNING: Try the cryptopals crypto challenges first!
Continuing the cryptopals crypto challenges with Set 2. Don’t read this unless you’re absolutely sure you don’t want to try them out yourself.
Notes for previous sets:
from binascii import unhexlify, b2a_base64, a2b_base64, hexlify
from Crypto.Cipher import AES
import random
import string
Challenge 9: Implement PKCS#7 padding¶
For some reason we didn’t google this and just used the example on the page to guide us, leading to some headaches many challenges later. Turns out the ‘\x04’ thing isn’t just a random byte, it’s because there needs to be 4 bytes of padding. Go figure.
The wiki said something about padding a full block extra if the string is already an even multiple of the block-size so that the padding can be detected even if ‘\x01’ is the last byte of the actual string.
def pkcs7_padding(byte_string: bytes, block_length: int) -> bytes:
num_to_pad = block_length - (len(byte_string) % block_length)
return byte_string + bytes([num_to_pad]) * num_to_pad
Challenge 10: Implement CBC mode¶
This was so much fun! Everything we know is from these pictures from the wiki
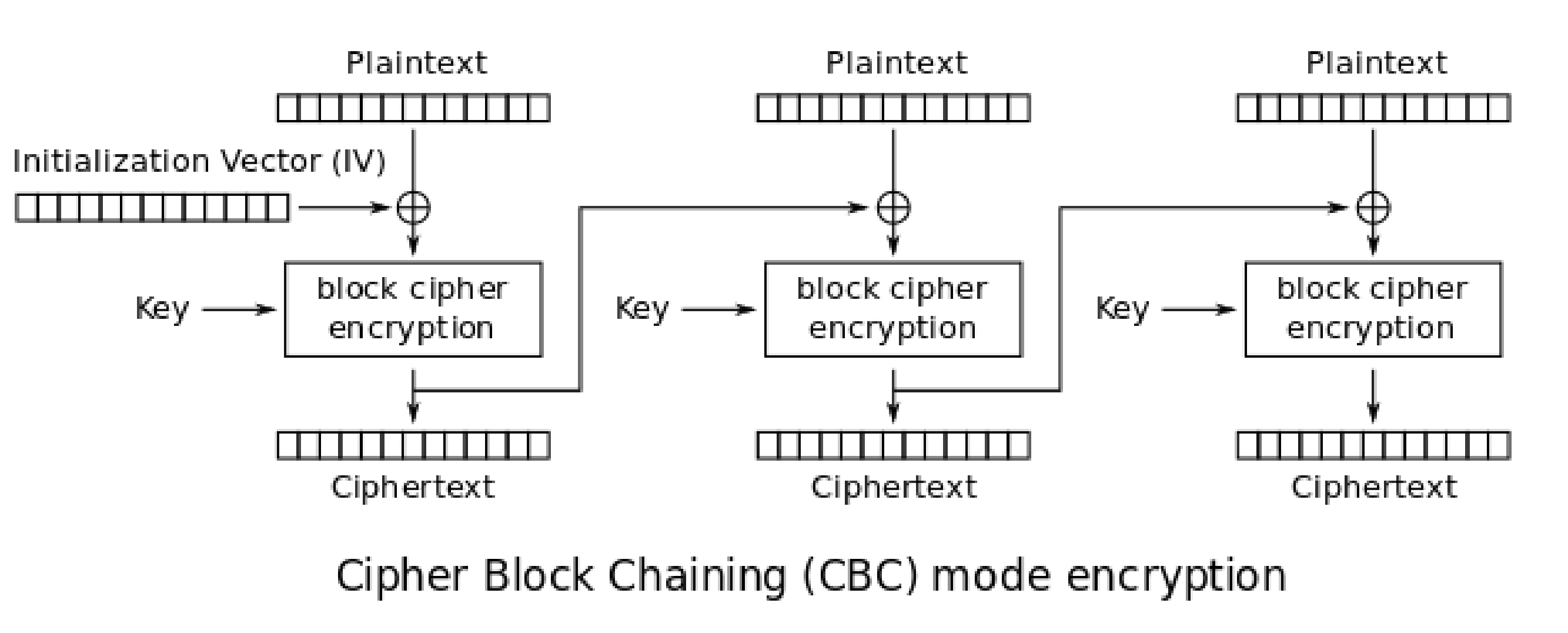
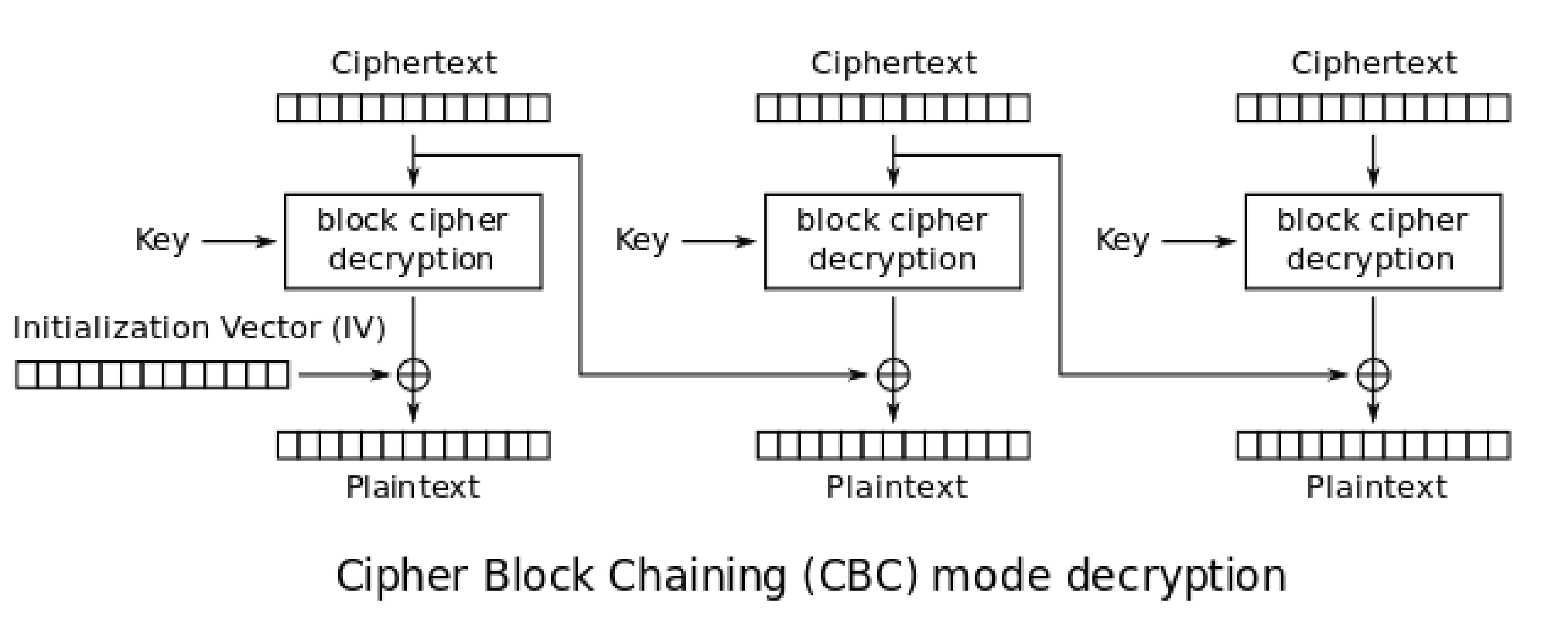
# Helper functions from the previous set
def fixed_xor(buffer1: bytes, buffer2: bytes) -> bytes:
return bytes([(b1 ^ b2) for b1, b2 in zip(buffer1, buffer2)])
def bytes_to_str(byte_list: bytes) -> str:
return "".join(filter(lambda x: x in string.printable, "".join(map(chr, byte_list))))
def aes_in_ecb_mode(byte_string: bytes, key: bytes, encrypt: bool = False) -> bytes:
cipher = AES.new(key, AES.MODE_ECB)
if encrypt:
return cipher.encrypt(byte_string)
else:
return cipher.decrypt(byte_string)
def cbc_mode(byte_string: bytes,
key: bytes,
initialization_vector: bytes,
encrypt: bool = True) -> bytes:
if encrypt:
previous_block = initialization_vector
cipher_text = b''
for i in range(0, len(byte_string), len(key)):
plain_text = fixed_xor(pkcs7_padding(byte_string[i: i + len(key)], len(key)),
previous_block)
previous_block = aes_in_ecb_mode(plain_text, key, encrypt=True)
cipher_text += previous_block
return cipher_text
else:
previous_block = initialization_vector
plain_text = b''
for i in range(0, len(byte_string), len(key)):
cipher_text = byte_string[i: i + len(key)]
plain_text += fixed_xor(aes_in_ecb_mode(cipher_text, key, encrypt=False), previous_block)
previous_block = cipher_text
return plain_text
byte_string = b''.join([a2b_base64(line.strip()) for line in open("data/crypto/10.txt").readlines()])
for line in bytes_to_str(cbc_mode(byte_string, b'YELLOW SUBMARINE', b'\x00'*16, encrypt=False)).split("\n")[:10]:
print(line)
I'm back and I'm ringin' the bell A rockin' on the mike while the fly girls yell In ecstasy in the back of me Well that's my DJ Deshay cuttin' all them Z's Hittin' hard and the girlies goin' crazy Vanilla's on the mike, man I'm not lazy. I'm lettin' my drug kick in It controls my mouth and I begin To just let it flow, let my concepts go
I almost want to listen to this song now.
Challenge 11: An ECB/CBC encryption oracle¶
Write a function that appends random stuff before and after your plaintext and then encrypts it with either CBC or ECB, who knows! (Well, we do since we wrote it but hey, not the point)
def generate_random_bytes(num_bytes: int) -> bytes:
return bytes([random.randint(0, 255) for _ in range(num_bytes)])
MODE_ECB = 0
MODE_CBC = 1
BLOCK_SIZE = 16
def encryption_oracle(byte_string: bytes) -> tuple:
append_before = generate_random_bytes(random.randint(5, 10))
append_after = generate_random_bytes(random.randint(5, 10))
plain_text = pkcs7_padding(append_before + byte_string + append_after, BLOCK_SIZE)
random_key = generate_random_bytes(BLOCK_SIZE)
method = random.randint(0, 1)
if method == MODE_ECB:
return aes_in_ecb_mode(plain_text, random_key, encrypt=True), MODE_ECB
else:
initialization_vector = generate_random_bytes(BLOCK_SIZE)
return cbc_mode(plain_text, random_key, initialization_vector, encrypt=True), MODE_CBC
Now we’ve to detect which mode the function is currently using assuming it’s totally closed-source and all you can do is change the input and look at the output. (This took me a while because it says block box in the question and I thought that meant you only get access to the final encrypted string, not the black box). Anyway, we have code for this from Challenge 8 (in Set 1)
# from Set 1
def detect_aes_in_ecb_mode(byte_string: bytes,
block_length: int) -> bool:
byte_blocks = [byte_string[i*block_length: (i+1)*block_length]
for i in range(int(len(byte_string) / block_length))]
unique_blocks = set(byte_blocks)
return len(unique_blocks)/len(byte_blocks) < 1
def decryption_oracle(encryptor) -> bool:
plain_text = b'a' * (BLOCK_SIZE * 5)
encrypted_string, mode = encryptor(plain_text)
if detect_aes_in_ecb_mode(encrypted_string, BLOCK_SIZE):
predicted_mode = MODE_ECB
else:
predicted_mode = MODE_CBC
return predicted_mode == mode
count = 0
for i in range(1000):
if decryption_oracle(encryption_oracle):
count += 1
count
1000
Challenge 12: Byte-at-a-time ECB decryption (Simple)¶
Here be dragons. Find the string an ECB encrypting function appends to yours before it does the encryption, given the function as a black box.
First off, here’s our black box:
GLOBAL_KEY = generate_random_bytes(BLOCK_SIZE)
UNKNOWN_STRING = b'Um9sbGluJyBpbiBteSA1LjAKV2l0aCBteSByYWctdG9wIGRvd24gc28gbXkg' \
b'aGFpciBjYW4gYmxvdwpUaGUgZ2lybGllcyBvbiBzdGFuZGJ5IHdhdmluZyBq' \
b'dXN0IHRvIHNheSBoaQpEaWQgeW91IHN0b3A/IE5vLCBJIGp1c3QgZHJvdmUg' \
b'YnkK'
def ecb_encryption_oracle(byte_string: bytes)->bytes:
unknown_string = a2b_base64(UNKNOWN_STRING)
plain_text = byte_string + unknown_string
return aes_in_ecb_mode(pkcs7_padding(plain_text, BLOCK_SIZE), GLOBAL_KEY, encrypt=True)
First we find the block size and the number of blocks the unkown string takes after padding.
for i in range(256):
if i == 0:
unknown_string_length = len(ecb_encryption_oracle(b'A'*i))
length_output = unknown_string_length
continue
new_length_output = len(ecb_encryption_oracle(b'A'*i))
block_size = new_length_output - length_output
if block_size != 0:
break
length_output = new_length_output
Let’s start with the first block of 16 bytes. We’ll make it 15 bytes of A. Then the last byte of this block becomes the first byte of the unknown string. We find this character by making a dict of the encrypted block for all possible last-byte characters. and checking it with the encrypted block of our 15 byte thing.
input_block = b'A'*15
last_byte_dict = {ecb_encryption_oracle(input_block + bytes([b]))[:16]: bytes([b]) for b in range(256)}
one_byte_short = ecb_encryption_oracle(b'A'*15)[:16]
first_unknown_byte = last_byte_dict[one_byte_short]
For the second byte of the unknown string, we make a block of 14 bytes of A, encrypt it, and check against the encrypted version of 14 A + first unknown byte + [all possible characters]. Once we know this we can do the third byte, and so on.
unknown_string_block = b''
input_block=b'A'*block_size # block size = 16
for n in range(block_size-1, -1, -1):
print(input_block)
input_block = input_block[1:]
last_byte_dict = {ecb_encryption_oracle(input_block + bytes([b]))[:block_size]: bytes([b]) for b in range(256)}
one_byte_short = ecb_encryption_oracle(b'A'*n)[:block_size]
last_byte = last_byte_dict[one_byte_short]
unknown_string_block += last_byte
input_block += last_byte
b'AAAAAAAAAAAAAAAA' b'AAAAAAAAAAAAAAAR' b'AAAAAAAAAAAAAARo' b'AAAAAAAAAAAAARol' b'AAAAAAAAAAAARoll' b'AAAAAAAAAAARolli' b'AAAAAAAAAARollin' b"AAAAAAAAARollin'" b"AAAAAAAARollin' " b"AAAAAAARollin' i" b"AAAAAARollin' in" b"AAAAARollin' in " b"AAAARollin' in m" b"AAARollin' in my" b"AARollin' in my " b"ARollin' in my 5"
Looking good.
Okay so now we just extend this to the next blocks, until we run out of characters. The concept remains the same except we look at a different part of the one_byte_short string now and use the b’A’s to position that block the way we want it.
def byte_at_a_time_ecb_decryption_simple(encryptor)->bytes:
for i in range(BLOCK_SIZE * 5): # This could be a while True if you really don't know the upper bound for your block size.
if i == 0:
unknown_string_length = len(encryptor(b'A'*i))
length_output = unknown_string_length
continue
new_length_output = len(encryptor(b'A'*i))
block_size = new_length_output - length_output
if block_size != 0:
break
length_output = new_length_output
if not detect_aes_in_ecb_mode(encryptor(b'A'*block_size*5), block_size):
return b'Not ECB Mode'
num_blocks = int(unknown_string_length/block_size)
unknown_string = b''
input_block = b'A'*block_size
for block_number in range(num_blocks):
unknown_string_block = b''
for n in range(block_size-1, -1, -1):
input_block = input_block[1:]
last_byte_dict = {encryptor(input_block + bytes([b]))[:block_size]: bytes([b]) for b in range(256)}
one_byte_short = encryptor(b'A'*n)[block_size*block_number: block_size*(block_number+1)]
if one_byte_short not in last_byte_dict:
break
last_byte = last_byte_dict[one_byte_short]
unknown_string_block += last_byte
input_block += last_byte
unknown_string += unknown_string_block
input_block = unknown_string_block
return unknown_string
for line in bytes_to_str(byte_at_a_time_ecb_decryption_simple(ecb_encryption_oracle)).split("\n"):
print(line)
Rollin' in my 5.0 With my rag-top down so my hair can blow The girlies on standby waving just to say hi Did you stop? No, I just drove by
Challenge 13: ECB cut-and-paste¶
Make an encrypted admin profile.
The example user profile in the question is “email=foo@bar.com&uid=10&role=user”, so naturally I assumed the function increments uid each time it’s called. Googled around a bit, found a way to do it using a global variable USER_ID set as itertools.count() and having the function call next(USER_ID). Of course this probably isn’t what the actual question had in mind, since that makes breaking it through cut-and-paste pretty tough.
Anyway, here’s how we parsed cookies.
def cookie_parsing_routine(input_cookie: (str, dict), encode=True)->(dict, str):
if encode:
return "&".join(["=".join([key, input_cookie[key]]) for key in ["email", "uid", "role"]])
else:
return {p.split("=")[0].strip(): p.split("=")[1].strip() for p in input_cookie.split("&")}
And here’s the boring, fixed uid profile maker. I chose to remove reserved characters.
def profile_for(email_id: str):
return cookie_parsing_routine({"email": email_id.replace("&", "").replace("=", ""),
"uid": '10',
"role": 'user'})
Encryption is just the normal ECB mode encryption.
def encrypt_user_profile(user_profile: bytes)->bytes:
return aes_in_ecb_mode(pkcs7_padding(user_profile, BLOCK_SIZE), GLOBAL_KEY, encrypt=True)
Decryption is ECB mode + our cookie parser.
def decrypt_user_profile(encrypted_profile: bytes)->dict:
return cookie_parsing_routine(bytes_to_str(aes_in_ecb_mode(encrypted_profile, GLOBAL_KEY, encrypt=False)), encode=False)
So that’s all our auxilliary functions done. Now how does one go about making an admin profile. We need to replace the encrypted version of role=user with an encrypted role=admin but these are different lengths so they won’t be encrypted the same way. So we just need to put them in different blocks of 16 bytes. role= can be in its own block and admin can be in one, with padding.
The fixed thing before role= is &uid=10&. Together they’re 13 bytes. We can control the remaining 3 using the email. We just need an email id
such that email=[email_id_first_half] is a multiple of 16 bytes and [email_id_second_half] is 3 bytes. With that we have email=[email_id]&uid=10&role= perfectly encrypted.
Then to find how admin is encrypted if padded to 16 bytes, we just make an email id that has admin in a separate block with artifical padding.
def ecb_cut_and_paste(encryptor, profile_maker)->bytes:
# admin in its own block
admin_email = b'a'*(BLOCK_SIZE - len("email=")) + pkcs7_padding(b'admin', BLOCK_SIZE)
# &role= ends block
num_blocks = int((len("&uid=10") + len("email=") + len("&role="))/BLOCK_SIZE) + 1
user_email = "a"*(num_blocks*BLOCK_SIZE - (len("&uid=10") + len("email=") + len("&role=")))
if len(user_email) < 10:
user_email += "a" * BLOCK_SIZE
user_email = user_email[:-10] + "@gmail.com"
admin_email_profile = encryptor(profile_maker(admin_email.decode()).encode("utf-8"))
user_profile = encryptor(profile_maker(user_email).encode("utf-8"))
admin_profile = user_profile[:num_blocks*BLOCK_SIZE] + admin_email_profile[BLOCK_SIZE:BLOCK_SIZE*2]
return admin_profile
decrypt_user_profile(ecb_cut_and_paste(encrypt_user_profile, profile_for))
{'email': 'aaa@gmail.com', 'uid': '10', 'role': 'admin'}
Challenge 14: Byte-at-a-time ECB decryption (Harder)¶
So now, in addition to adding an unknown string after your plaintext, the ECB encryptor also adds random bytes before your plaintext.
MAX_SIZE = BLOCK_SIZE * 10
RANDOM_BYTES = generate_random_bytes(random.randint(1, int(MAX_SIZE/2)))
def ecb_encryption_oracle_harder(byte_string: bytes)->bytes:
unknown_string = a2b_base64(UNKNOWN_STRING)
plain_text = RANDOM_BYTES + byte_string + unknown_string
return aes_in_ecb_mode(pkcs7_padding(plain_text, BLOCK_SIZE), GLOBAL_KEY, encrypt=True)
If we knew exactly how many bytes long the random thing is, we could just use the same idea as in Challenge 12, the only difference being we account for those extra bytes.
First we find out how many blocks the random string takes by finding the smallest number of blocks > the longest common prefix of two encrypted strings.
from os.path import commonprefix
def find_block_size(encryptor):
length_output = len(encryptor(b'A'*0))
for i in range(1, MAX_SIZE):
new_length_output = len(encryptor(b'A'*i))
block_size = new_length_output - length_output
if block_size != 0:
break
length_output = new_length_output
return length_output, block_size
def find_num_random_blocks(encryptor, length_output, block_size):
common_prefix_length = len(commonprefix([encryptor(b''), encryptor(b'A')]))
for num_random_blocks in range(int(length_output/block_size)):
if common_prefix_length < block_size * num_random_blocks:
break
return num_random_blocks
Then, we see how many ‘A’s we have to add to achieve this num_random_blocks.
def find_string_lengths(encryptor, block_size, num_random_blocks):
encrypted_strings =[]
for i in range(block_size):
encrypted_strings.append(encryptor(b'A'*i))
random_string_length = len(commonprefix(encrypted_strings))
unknown_string_length = len(encrypted_strings[0]) - random_string_length
if len(encrypted_strings) > 1 and random_string_length >= block_size * num_random_blocks and random_string_length % block_size == 0:
min_addition = i-1
break
encrypted_strings = [encrypted_strings[-1]]
return min_addition, random_string_length, unknown_string_length
This is possibly more convoluted than it needs to be, I’m not sure.
Now we just add this min_addition when making our every possible last byte dict. And, when finding the part of the encrypted string to look at, we offset by random_string_length.
def byte_at_a_time_ecb_decryption_harder(encryptor)->bytes:
length_output, block_size = find_block_size(encryptor)
num_random_blocks = find_num_random_blocks(encryptor, length_output, block_size)
min_addition, random_string_length, unknown_string_length = find_string_lengths(encryptor, block_size, num_random_blocks)
if not detect_aes_in_ecb_mode(encryptor(b'A'*MAX_SIZE), block_size):
return b'Not ECB Mode'
num_blocks = int(unknown_string_length/block_size)
unknown_string = b''
input_block = b'A'*(block_size + min_addition)
for block_number in range(num_blocks):
unknown_string_block = b''
for n in range(min_addition + block_size - 1, min_addition - 1, -1):
input_block = input_block[1:]
last_byte_dict = {encryptor(input_block + bytes([b]))[random_string_length: random_string_length + block_size]: bytes([b]) for b in range(256)}
offset = (block_size * block_number) + random_string_length
one_byte_short = encryptor(b'A'*n)[offset: offset + block_size]
if one_byte_short not in last_byte_dict:
break
last_byte = last_byte_dict[one_byte_short]
unknown_string_block += last_byte
input_block += last_byte
unknown_string += unknown_string_block
input_block = b'A'*min_addition + unknown_string_block
return unknown_string
for line in bytes_to_str(byte_at_a_time_ecb_decryption_harder(ecb_encryption_oracle_harder)).split("\n"):
print(line)
Rollin' in my 5.0 With my rag-top down so my hair can blow The girlies on standby waving just to say hi Did you stop? No, I just drove by
Challenge 15: PKCS#7 padding validation¶
This is the point where we realized our initial padding function (which just appended a random byte) was wrong, went back and fixed it, and then spent a while fixing all the challenges after it. Anyway, we take the last byte and check that all the bytes from the back, upto the number the last byte represents, are all that same last byte
byte_string = b'ICE ICE BABY\x01\x02\x03\x04'
last_byte = byte_string[-1]
for i in range(last_byte, 0, -1):
if byte_string[-i] != last_byte:
raise ValueError("bad padding")
--------------------------------------------------------------------------- ValueError Traceback (most recent call last) <ipython-input-27-1e54fd0d7f4e> in <module> 3 for i in range(last_byte, 0, -1): 4 if byte_string[-i] != last_byte: ----> 5 raise ValueError("bad padding") ValueError: bad padding
def pkcs7_padding_validation(byte_string: bytes)->bytes:
last_byte = byte_string[-1]
if last_byte > len(byte_string):
return ValueError("bad padding")
for i in range(last_byte, 0, -1):
if byte_string[-i] != last_byte:
raise ValueError("bad padding")
return byte_string[:-last_byte]
Challenge 16: CBC bitflipping attacks¶
Make an admin account in CBC mode.
The encryptor adds a prefix and a suffix to our plaintext and then quotes out all ;s and =s, before encrypting in CBC mode. The checker decrypts the input and checks if ;admin=true; is in it. The task is manipulate an encrypted string such that it passes the checker.
Here’s our encryptor and checker functions.
RANDOM_INITIALIZATION_VECTOR = generate_random_bytes(BLOCK_SIZE)
def cbc_bitflipping(byte_string: bytes, encrypt=True)->bytes:
if encrypt:
prefix = b'comment1=cooking%20MCs;userdata='
suffix = b';comment2=%20like%20a%20pound%20of%20bacon'
input_string = (prefix + byte_string + suffix).replace(b';', b'";"').replace(b'=', b'"="')
return cbc_mode(pkcs7_padding(input_string, BLOCK_SIZE), GLOBAL_KEY, RANDOM_INITIALIZATION_VECTOR, encrypt=True)
else:
return cbc_mode(byte_string, GLOBAL_KEY, RANDOM_INITIALIZATION_VECTOR, encrypt=False)
def cbc_bitflipping_check(byte_string:bytes)->bool:
decrypted_string = cbc_bitflipping(byte_string, encrypt=False)
if b';admin=true;' in decrypted_string:
return True
else:
return False
The clue is that a bit error in CBC mode scrambles the block the error is in (on decryption) but transmits the error to the same position in the next block. The flowchart from the wiki comes in handy again:

To make a block of plaintext - the previous block’s ciphertext is XORed with the current block’s ECB decrypted ciphertext.
Say ciphertext_block_1 is “xxxx” (assuming block size 4 for now, even though AES needs minimum 16) and ciphertext_block_2 is “ghjk”. Then plaintext_block_2 = decrypt_ECB("ghjk") $\oplus$ “xxxx”.
If we change ciphertext_block_1 to “xxbx”, plaintext_block_2 becomes decrypt_ECB("ghjk") $\oplus$ “xxbx”, i.e only the 3rd position changes.
Suppose we know plaintext_block_2, it’s “bird” (somehow). Cacofonix would like it to be “bard”. He needs to find a byte “y” such that he can change ciphertext_block_1 to “xyxx” and get “bard” as plaintext_block_2.
decrypt_ECB("ghjk") $\oplus$ “xxxx” = “bird”
decrypt_ECB("ghjk") $\oplus$ “xyxx” = “bard”
Let’s say $h*$ is the ECB decrypted “h”. Also, the inverse of XOR is XOR.
$$h^* \oplus x = \text{“i”}$$$$h^* = x \oplus \text{“i”}$$$$h^* \oplus y = \text{“a”}$$$$y = h^* \oplus \text{“a”} = x \oplus \text{“i”} \oplus \text{“a”}$$Back to our question, we can input “xadminxtruex” to our encryptor and then change the xs into ;s and =s. For this we first need to make sure our admin input is in a separate block, which we do by adding a bunch of As before it, so that all of the prefix is padded upto a multiple of the block size. Then we need to identify the block previous to the admin block. Then, at positions 0, 6, and 11 on this previous block (these are the positions of the xs in the admin block), we use our bitflipping formula from above to make them into “;”, “=”, and “;” respectively.
def cbc_bitflipping_attack(encryptor, checker):
# Number of blocks taken up by the prefix:
num_prefix_blocks = len(commonprefix([encryptor(b''),
encryptor(b'A')])) // BLOCK_SIZE + 1
# Number of extra letters to add such that
# the prefix + extra takes up a whole number of blocks
encrypted_strings = [encryptor(b'A'*0)]
min_addition = None
for i in range(1, BLOCK_SIZE):
encrypted_strings.append(encryptor(b'A'*i))
length_common_prefix = len(commonprefix(encrypted_strings))
if length_common_prefix == num_prefix_blocks*BLOCK_SIZE:
min_addition = i-1
break
encrypted_strings = [encrypted_strings[-1]]
assert min_addition is not None
encrypted = encryptor(b'A'*min_addition + b'xadminxtruex')
previous_block = [p for p in encrypted[(num_prefix_blocks-1)*BLOCK_SIZE: num_prefix_blocks*BLOCK_SIZE]]
previous_block[0] ^= ord(b'x') ^ ord(b';')
previous_block[6] ^= ord(b'x') ^ ord(b'=')
previous_block[11] ^= ord(b'x') ^ ord(b';')
previous_block = bytes(previous_block)
admin_string = encrypted[:(num_prefix_blocks-1)*BLOCK_SIZE] + previous_block + encrypted[num_prefix_blocks*BLOCK_SIZE:]
return checker(admin_string)
cbc_bitflipping_attack(cbc_bitflipping, cbc_bitflipping_check)
True
And that’s Set 2.
Here’s Set 3