Everyone who’s interested in programming has probably had a brush with Conway’s Game of Life in some way or the other. It’s a cellular automata system renowned for it’s elegantly simple rules and the incredible complexity it produces. We started playing around with it after seeing this post about a game of life instance running inside game of life, and this stackexchange post where some brilliant people, when tasked with getting Tetris to run inside game of life, decided to build a whole computer inside it which, incidentally, could play Tetris.
Here’s a quick rundown of the rules: Each cell in the grid is either dead (0) or alive (1). The neighbors of a cell are the ones adjacent (diagonally or orthogonally) to it, i.e a 3x3 grid with the cell in the center. The rule system for the game of life is commonly described as B3/S23. This means a cell is born if it has 3 neighbors and survives a round if it has 2 or 3 neighbors, otherwise it dies. You can initialize the grid with any pattern of 1s and 0s.
The initial plan was to get the game of life running and then jump straight into building logic gates, but the rule system was so incredibly simple and extensible that it was just crying out to be experimented with. A short and woefully incomplete list of possible changes to these initial rules:
- changing B and S
- changing the size and dimensions of the neighborhood
- changing the starting state
- using floats instead of ints to weight the influence of each neighbor
- giving a cell more than 2 possible states
- and, of course, running multiple rule sets one after each other on the same start grid
Implementation¶
We made a reasonably fast implementation of Conway’s Game of Life in Python, specifically with changing some of the parameters in mind.
import numpy as np
from scipy.ndimage.filters import convolve
from skimage.morphology import disk
from matplotlib import pyplot as plt
from dataclasses import dataclass
@dataclass
class Parameters:
birth: list
survive: list
neighborhood_width: int = 3
neighborhood_height: int = 3
kernel_shape: str = "square"
def get_kernel(self):
if self.kernel_shape == "square":
# neighbors are in a grid of height*width around a cell, not including the cell
self.kernel = np.ones((self.neighborhood_height, self.neighborhood_width))
self.kernel[self.neighborhood_height//2, self.neighborhood_width//2] = 0
elif self.kernel_shape == "disk":
# neighbors are in a circular disk with radius height/2 (=width/2) around a cell, not including the cell
assert self.neighborhood_height == self.neighborhood_width
self.kernel = disk(self.neighborhood_height//2)
else:
self.kernel = np.ones(self.neighborhood_height, self.neighborhood_width)
class CellularAutomata:
def __init__(self, init_world: np.ndarray, parameters: Parameters, cmap: str="gray"):
self.height, self.width = init_world.shape
self.world = init_world
self.memory = np.array(self.world, dtype=np.float64)
self.cmap = cmap
self.set_parameters(parameters)
def set_parameters(self, parameters):
self.parameters = parameters
self.parameters.get_kernel()
def procreate(self):
"""
calculates the next round, params same as iterate
"""
new_world = np.array(self.world, dtype=np.float64)
# finds the sum of the values of the neighbors
neighbors = convolve(new_world, self.parameters.kernel, mode='constant')
# checks which dead cells have enough live neighbors to come back alive in the next round
birth_filter = np.logical_or.reduce([(b0 - 1 < neighbors) & (neighbors < b1 + 1) for b0, b1 in self.parameters.birth]) & (new_world < 0.5)
# checks which live cells have enough live neighbors to survive to the next round
survive_filter = np.logical_or.reduce([(s0 - 1 < neighbors) & (neighbors < s1 + 1) for s0, s1 in self.parameters.survive]) & (new_world > 0.5)
new_world[...] = 0
new_world[birth_filter | survive_filter] = 1
self.world = new_world
self.memory += self.world
def iterate(self, n_iter: int, plot: bool=False, plot_memory: bool=False):
"""
Runs the world and plots.
n_iter: number of iterations
plot: if True, plots each iteration
plot_memory:
if True, plots matrix sum of all previous iterations + current iteration
instead of just the current iteration
"""
old_world = np.array(self.world)
for _ in range(n_iter):
if not np.any(self.world):
break
self.procreate()
# stop if the world has stabilized
if np.array_equal(self.world, old_world):
break
old_world = np.array(self.world)
if plot:
self.plot(memory=plot_memory)
def plot(self, memory: bool=False):
"""
Plot the world. If memory is True, then plot the matrix sum of all previous iterations
"""
if memory:
plt.imshow(self.memory, cmap=self.cmap)
else:
plt.imshow(self.world, cmap=self.cmap)
plt.axis('off')
plt.show()
To calculate the neighbors of a particular cell in a grid, we used the convolve function from scipy.ndimage on a kernel which is a 3x3 grid of 1s, except the center which is a 0. This is the equivalent of finding the diagonally/orthogonally adjacent indices of a cell and adding their values. Both
scipy.signal.convolve and scipy.signal.convolve2d can be used for the same purpose but the former, which may be a bit faster as it uses fft, tends to make floats like 5.000003 which can make things mildly unpredictable, and the latter is super slow.
The memory part isn’t needed for vanilla game of life but we use it later for our experiments and it makes for some really cool looking plots.
You can also control a bit how lively your initial world is by increasing/decreasing the probability of a cell being alive:
def create_random_world(height: int, width: int, life_probability: float=0.5):
return np.random.choice(np.array([0, 1], dtype=np.float64),
(height, width),
p=[life_probability, 1.-life_probability])
Variations on Life¶
Here’s the original game of life. Setting birth to (3,3) implies that a dead cell with 3 live neighbors comes alive. survive=[(2,3)] means a live cell with 2-3 (inclusive) live neighbors lives, otherwise it dies. This is a list of tuples, so you can add more ranges to shake things up.
init_world = create_random_world(10, 10)
life_parameters = Parameters(birth=[(3, 3)], survive=[(2, 3)])
life = CellularAutomata(init_world, life_parameters)
life.iterate(5, plot=True, plot_memory=False)
Here’s a cool set of parameters we found that results in a sort of bone-like pattern. memory=True means that every new iteration is added onto the old one, instead of starting from scratch. This leads to a slow accumulation of life in each cell which creates a nice shaded effect.
init_world = create_random_world(250, 250, 0.4)
bones_parameters = Parameters(birth=[(8, 17)], survive=[(12, 13)],
neighborhood_height=5, neighborhood_width=5)
bones = CellularAutomata(init_world, bones_parameters)
bones.iterate(500)
plt.figure(figsize=(10,10))
bones.plot(memory=True)
Here’s another:
init_world = create_random_world(250, 250, 0.4)
fire_parameters = Parameters(birth=[(8, 17)], survive=[(11, 14)],
neighborhood_height=7, neighborhood_width=3)
fire = CellularAutomata(init_world, fire_parameters, cmap="copper")
fire.iterate(500)
plt.figure(figsize=(10,10))
fire.plot(memory=True)
Layering automata on top of each other (using set_parameters) leads to some pretty neat textures and pictures.
circle_parameters = Parameters(birth = [(11, 41)], survive = [(21, 42)],
neighborhood_width = 12, neighborhood_height = 12,
kernel_shape="disk")
init_world = create_random_world(500, 500, 0.5)
circles = CellularAutomata(init_world, circle_parameters, cmap="gray_r")
circles.iterate(15)
plt.figure(figsize=(10,10))
circles.plot(memory=True)
vein_parameters = Parameters(birth = [(25, 49)], survive = [(20, 40)],
neighborhood_width = 7, neighborhood_height = 7)
halo_parameters = Parameters(birth = [(10, 40)], survive = [(20, 39)],
neighborhood_width = 7, neighborhood_height = 7)
circles.set_parameters(vein_parameters)
circles.iterate(7)
circles.set_parameters(halo_parameters)
circles.iterate(7)
plt.figure(figsize=(10,10))
circles.plot(memory=True)
Some experimentation (varying parameters, layering random automata, changing color maps etc.) led to some brilliant, wallpaper-worthy patterns (The full size images are in this flickr album):
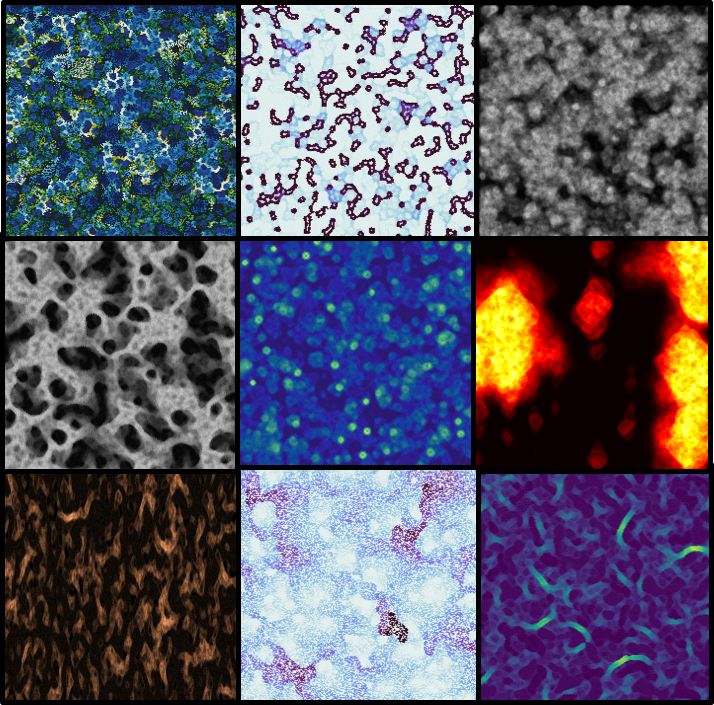
Next step¶
A genetic algorithm to discover good parameter combinations.